58.2M
79.4M
326m
27 MB
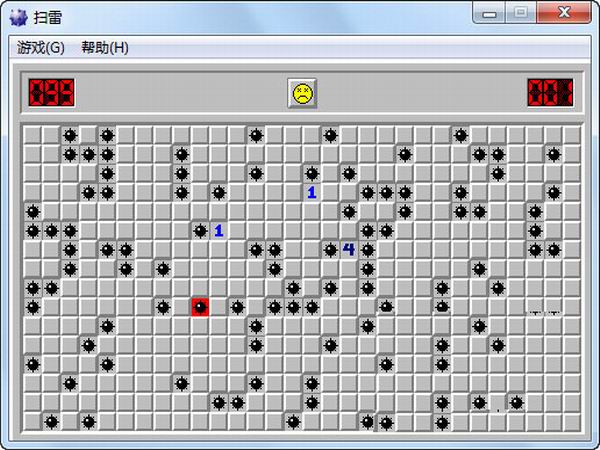
扫雷游戏是微软推出的一款非常有趣的益智游戏。是Windows平台下非常经典的小游戏。相信很多用户都玩过这个游戏？游戏的目标是根据点击方块时出现的数字，在最短的时间内找出所有非雷方块，同时避免踩雷。游戏中有各种难度挑战。欢迎下载体验。
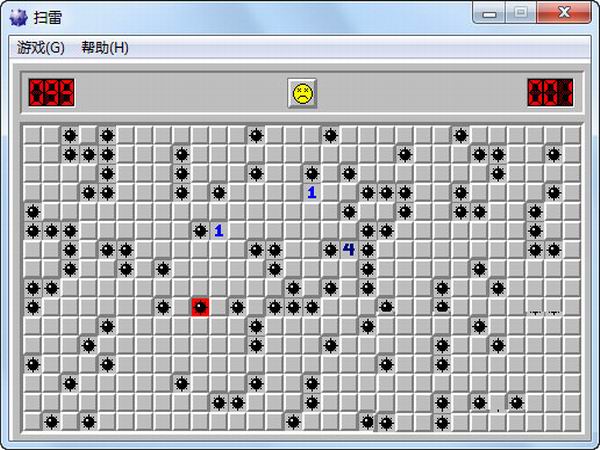
很多人接触的第一个游戏可能是扫雷，自带windows操作系统。作为一款非常经典的益智游戏，《扫雷》以其简单的玩法广受好评。这次是最经典的扫雷舰，也是最受欢迎的版本。它的外形更酷，还增加了爆炸音效。它的游戏很简单，但是很考验逻辑能力。
[扫雷基本介绍]
1.三个难度等级:低、中、高。2.地雷的面积和数量可以定制。
3.如果你觉得是打雷，可以用小旗做个标记，就不怕不小心点着了。
4.如果标记了小旗子，感觉不像打雷，可以再点一下变成问号模式。再点一下，问号又会消失。
左键点击:在判断不是雷霆的方块上点击左键打开方块。如果一个数字出现在一个方块上，表示其周围3×3区域内的地雷数量(一般为8个方块，边块5个方块，角块3个方块)。所以扫雷数量最多的是8个)；如果方块为空(相当于0)，可以递归打开与空相邻的方块；如果雷声响起，游戏就结束了。
右键:在判断为地雷的方块上按下右键，标记地雷(显示为小红旗)。重复一次或两次以取消标记(如果“标记(？)”，需要两次操作才能取消标记)。
双击:同时按下左键和右键，完成双击。当双击位置周围标记的地雷数量与该位置的数量相等时，操作有效，相当于左键单击该数量周围未打开的方块一次。局部雷霆未完全标记时双击无效。如果数字周围有错误标记的地雷，游戏就结束了将显示在错误标记的地雷上。
扫雷怎么玩？
开始时，用鼠标左键随机点击一个方块，方块将被打开，并显示方块中的数字。方块表示周围的八个方块中隐藏着几个地雷。用鼠标右键标记雷霆，同时按左右键完成双击。当双击位置周围标记的地雷数量与该位置的数量相等时，操作有效，相当于左键单击该数量周围未打开的方块一次。局部雷霆未完全标记时双击无效。如果数字周围有错误标记的地雷，游戏结束，错误标记的地雷上会显示一个“×”。
扫雷的核心理念:九宫格。
圆圈中的“1”表示其周围的八个网格中只有一个地雷，因此我们将右键单击未显示为地雷的剩余网格(红旗)。
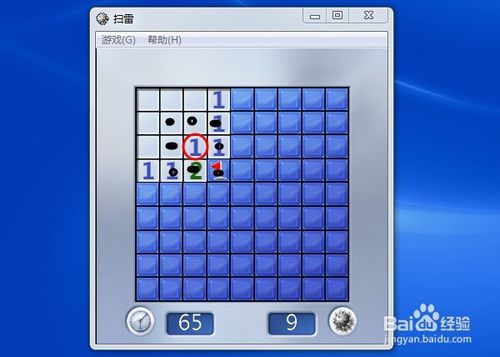然后，发现红旗上方也有一个“1”，它所代表的雷已经被标注出来。然后，当我们同时用左右键按下这个数字时，它右边的三个方块就会同时打开。
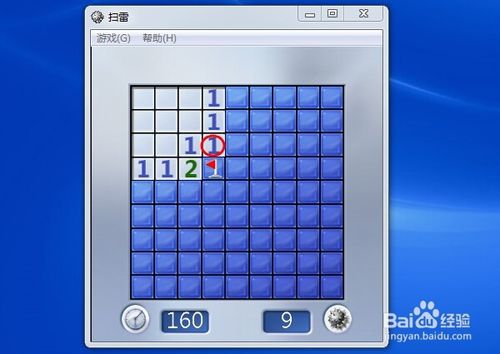这是另一个想法。我们在标记一个雷的时候，可以以这个雷为中心，在它周围的八个方块中找到数字，去一一对应。
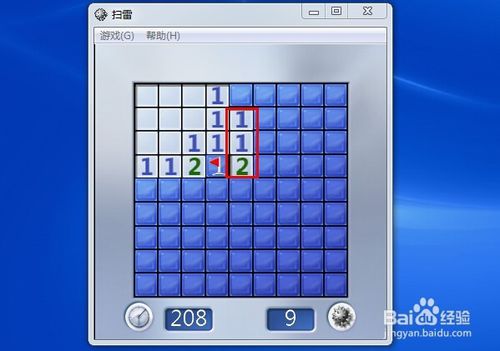如图所示。我们在红旗的右上角发现了一个“1”。重复操作，同时用左右键按下该数字。
该图标出现并继续重复操作。玩几局就熟了。
1.如果你不能确定一个方块中是否有雷，请右击两次并使用问号(？)。稍后，您可以右键单击方块一次以将其标记为地雷，或者右键单击方块两次以移除标记。2.如果一个数字方块周围的所有地雷都被标记出来，你可以指向该方块，同时单击鼠标左键和右键来挖掘其周围剩余的方块。如果编号方块周围的地雷没有全部标记，同时点击两个按钮，其他隐藏或未标记的方块会被按一次(即闪烁一次)。
3.寻找常见的数字组合，通常代表常见的地雷组合。例如，一组未切割的正方形边上的三个相邻数字2-3-2表示这三个数字旁边有三个地雷。
如何判断扫雷
1.1°角对应的角度一定是雷，这也是扫雷中最常见的情况。
2.侧面两个2对应的两个区块一定是雷霆。
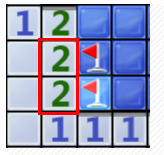
3.角3对应的三块一定是雷。
4.隔离3对应的三件一定是雷霆。
5.孤立的4对应的4块一定是雷。
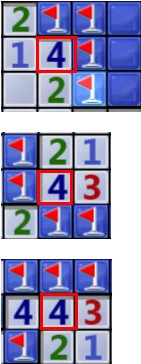
6.孤立的五个对应的五个一定是雷。
7.两个1，一个1和一个2。两个1下面对应的块一定是雷霆。
8.隔离2对应的两块一定是雷霆。
9.已知3的左边两个是雷霆，那么3的底部两个一定有一个是雷霆，那么第二个1下面的块肯定不是雷霆。
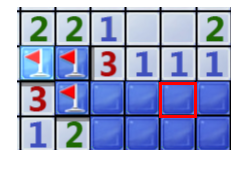
10.已知2左边的是雷霆，那么2最下面的两个一定有一个是雷霆，然后1右边的三个块没有一个是雷霆。
11.顶部1对应的两个角块中有一个是雷霆，所以底部1下面的三个块不是雷霆。
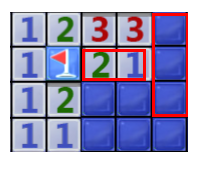
12.两个并排的3对应的3块都是雷。
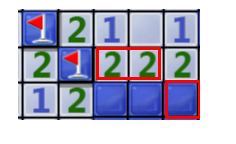
13.两个2并排。已知左2的左边是雷，那么右2的右下角一定也是雷。
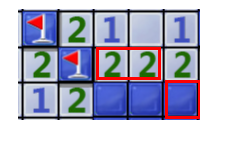
14.如果已知右边两个竖1和左边两个块都是雷，那么左边两个1下面的两个块就不是雷。
5，1，2是隔离排列的，所以2要从下面的三个块中选择两个块，肯定不会是左边的两个，所以2右下角的那个肯定是射线，而1和2下面的两个块中有一个是射线，所以1左下角的那个肯定不是射线。
16.A 3和a 2是并排的。知道上面是雷霆，左下角的块肯定是雷霆，右下角的块肯定不是雷霆。
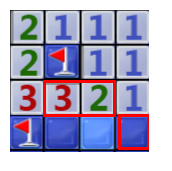
17.两个2是并排的。已知右2正上方的块是射线，所以两个左2只有一个是射线，左2的三个左块都不是射线。
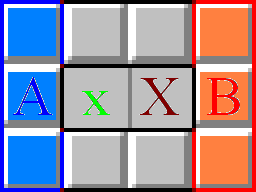
[扫雷基本公式]如上图:大x和小x分别代表两个已知的相邻数，周围方块的个数设置如下:A区块数为A，B区块数为B，A区矿数为A，B区矿数为B，公共区域矿数为n。
当x = x+b时，B区的方块都是雷，A区的方块都是数。
演示过程:
原始假设:x > n┓
┣ X>n+B ┓
X=x+B ┛ ┣ n+b>n+B → b>B
X=n+b ┛
显然，b < = b ∴的原始假设不成立→ x = n┓
┣ a=0
X = n+ one┛
X =┓北部
X=x+B ┣ n+B=n+b → B=b
X=n+b ┛
获得论文证书(以上认证过程中未标注雷子，标注的雷子也视为正方形)
皇家骑士团：重生它现在位于PS5/PS4/PC/NS上。
蝙蝠侠配音演员凯文·康瑞去世，享年66岁。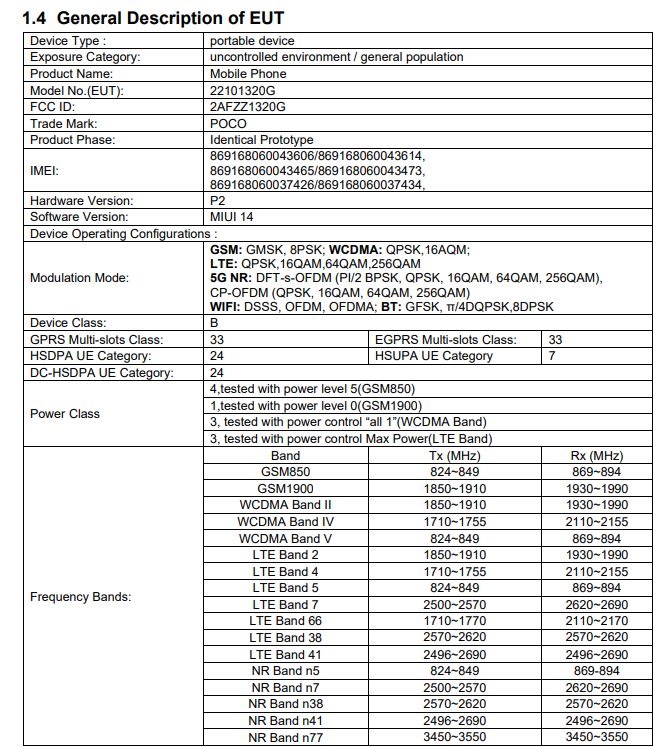
小米POCOX5首次曝光:开机是MIUI14
首款国产游戏显卡来摩尔线程MTTS80，售价2999元。
Twitter信任和安全部门主管离职，销售经理撤回辞呈
8家日本公司联合成立半导体公司Rapidus，制造高级芯片。
博德之门3将于2023年正式发售。更多信息将于12月发布。
小米迄今为止最薄的笔记本，双十一就卖出去了！JD.COM销售额排名第一。
